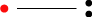普段、我々が使用するサイコロは1〜6の目を持つ立方体である。
これを3次元サイコロとする。
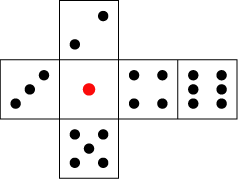
おなじみ3次元サイコロの展開図を以下に示す。
立方体を3次元以外のものに拡張したものを超立方体というそうだ。3次元以外の超立方体でサイコロを考えてみよう。
超立方体の特徴
Wikipediaの記事によれば、超立方体の特徴は以下のようになる。 n次元超立方体の
- 頂点の数:2n
- 辺の数:n・2n-1
- 面の数:nC2・2n-2
- 胞(立方体)の数:nC3・2n-3
- k次元胞の数:nCk・2n-k
1辺の長さがLの場合
- 体積:Ln
- 表面積:2nLn-1
- 対角線の長さ:L√n
また、3次元サイコロを分析すると以下の特徴がある。
- 目は面に対応する
- 目の数をnとして、ある目xは(n+1)-xの目以外の目に接する
こうした特性を鑑み、3次元以外のサイコロを考えてみた。
4次元サイコロ
4次元サイコロは以下のようになる。
4次元超立方体の
- 頂点の数:16
- 辺の数:32
- 面の数:24
- 胞(立方体)の数:8
1辺の長さがLの場合
- 体積:L4
- 表面積:8L3
- 対角線の長さ:2L
4次元超立方体の体積・表面積・対角線の長さってどこを測るのかよくわからんが、こんな感じか。
- 体積: 普通イメージする3次元の量でなく4次元の量。たとえば辺の長さLの単位がmならこの体積の単位はm4のはず。
- 表面積: 構成する立方体の体積の総和。
- 対角線の長さ: わからん。その物体内で取りうる最も長い線分の長さ、ということか。もはやイメージ不能だ。
サイコロとしての特徴は以下の通り
- 目は胞(立方体)に対応する。上記の通りその数は8
- ある目xは9-xの目以外の目に接する
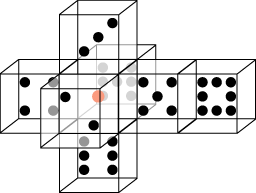
こうして考えられる4次元サイコロだが、4次元のものを2次元で描くのは私の技量を超えるので、その展開図(3次元になる)の俯瞰図を示す。
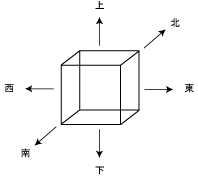
なお、下図のように方向を名付けると、上図における各々の目は以下のように接することとなる。
| 目 | 上 | 下 | 東 | 西 | 南 | 北 |
|---|---|---|---|---|---|---|
| 1 | 3 | 6 | 5 | 4 | 2 | 7 |
| 2 | 3 | 6 | 5 | 4 | 8 | 1 |
| 3 | 8 | 1 | 5 | 4 | 2 | 7 |
| 4 | 3 | 6 | 1 | 8 | 2 | 7 |
| 5 | 3 | 6 | 8 | 1 | 2 | 7 |
| 6 | 1 | 8 | 5 | 4 | 2 | 7 |
| 7 | 3 | 6 | 5 | 4 | 1 | 8 |
| 8 | 6 | 3 | 4 | 5 | 7 | 2 |
2次元サイコロ
2次元サイコロは以下のようになる
2次元超立方体の
- 頂点の数:4
- 辺の数:4
- 面の数:1
1辺の長さがLの場合
- 体積:L2
- 表面積:4L
- 対角線の長さ:L√2
ようは正方形ですな。
- 体積: 面積
- 表面積: 構成する辺の長さの総和、と考えるべし。
サイコロとしての特徴は以下の通り
- 目は辺に対応する。上記の通りその数は4
- ある目xは5-xの目以外の目に接する
以下が2次元サイコロの例。
なお、3次元空間中で使用する場合は、ちょっと工夫が必要。
1次元サイコロ
1次元サイコロは以下のようになる
1次元超立方体の
- 頂点の数:2
- 辺の数:1
1辺の長さがLの場合
- 体積:L
- 表面積:2
- 対角線の長さ:L
物体としては長さLの線分・・・なのかな。
うん?体積→長さ、として「表面積2」ってなんだ。
この場合、長さの1次元下の量だから、たとえばLの単位がmとしたらm0になって、もうなにがなにやら。
いや、0次元=点の量なんだから、この場合構成する頂点の数になるわけか。うーむ。
対角線の長さLは当然。
サイコロとしての特徴は以下の通り
- 目は頂点に対応する。上記の通りその数は2
- ある目xは3-xの目以外の目に接する(そんな目はない)
以下が1次元サイコロの例。
これも、3次元空間中で使用する場合は、ちょっと工夫が必要。
たとえば、こんな風に作る。
いや、コイン使えよって話ですが。
0次元サイコロ
一応当てはめてみる。
0次元超立方体の
- 頂点の数:1
1辺の長さがLの場合
- 体積:1
- 表面積:0
- 対角線の長さ:0
点です。0次元なのでそれしかありえない。
体積=点の量なので、頂点と一致。
表面積は-1次元を想定しないといけないので、イメージ不能。
対角線の長さ0は納得。
サイコロとしての特徴は以下の通り
- 目は何に対応するか不明。
- ある目xは2-xの目以外の目に接する(そんな目はない)
目は-1次元のものに対応するわけだが、想定不能。
まあ点なので、目は1つと考えよう(てきとー)。
以下が0次元サイコロの例。
大きさのない点では描きようがないので、球です。
もちろん、いくら転がしても1しか出ません。
なお、今回nCkでn<kの場合、解なしとした。高校数学しか知らないのでわからん。あと、小数次元も考えていない。負の次元を想定するのかも不明。